Править] Классификация методов оптимизации

Методы оптимизации классифицируют в соответствии с задачами оптимизации:

Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.
Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.

Существующие в настоящее время методы поиска можно разбить на три большие группы:

детерминированные;
случайные (стохастические);
комбинированные.

По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.

По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:

Задачи оптимизации, в которых целевая функция 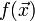и ограничения 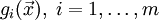являются линейными функциями, разрешаются так называемыми методами линейного программирования.
В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:

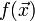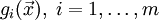если и — выпуклые функции, то такую задачу называют задачей выпуклого программирования;
если , то имеют дело с задачей целочисленного (дискретного) программирования.

По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:

прямые методы, требующие только вычислений целевой функции в точках приближений;
методы первого порядка: требуют вычисления первых частных производных функции;
методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.

Помимо того, оптимизационные методы делятся на следующие группы:

аналитические методы (например, метод множителей Лагранжа и условия Каруша-Куна-Таккера);
численные методы;
графические методы.

В зависимости от природы множества X задачи математического программирования классифицируются как:

задачи дискретного программирования (или комбинаторной оптимизации) — если X конечно или счётно;
задачи целочисленного программирования — если X является подмножеством множества целых чисел;
задачей нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерного векторного пространства.
Если же все ограничения и целевая функция содержат лишь линейные функции, то это — задача линейного программирования.

Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование. Математическое программирование используется при решении оптимизационных задач исследования операций.

Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:

Определение границ системы оптимизации

Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается

Выбор управляемых переменных

«Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)

Определение ограничений на управляемые переменные

… (равенства и\или неравенства)

Выбор числового критерия оптимизации

Создаём целевую функцию

Править] История

Задачи линейного программирования были первыми, подробно изученными задачами поиска экстремума функций при наличии ограничений типа неравенств. В 1820 г. Ж. Фурье и затем в 1947 г. Дж. Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод, ставший основным при решении задач линейного программирования.

Присутствие в названии дисциплины термина «программирование» объясняется тем, что первые исследования и первые приложения линейных оптимизационных задач были в сфере экономики, так как в английском языке слово «programming» означает планирование, составление планов или программ. Вполне естественно, что терминология отражает тесную связь, существующую между математической постановкой задачи и её экономической интерпретацией (изучение оптимальной экономической программы). Термин «линейное программирование» был предложен Дж. Данцигом в 1949 г. для изучения теоретических и алгоритмических задач, связанных с оптимизацией линейных функций при линейных ограничениях. Поэтому наименование «Математическое программирование» связано с тем, что целью решения задач является выбор оптимальной программы действий.

Выделение класса экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, следует отнести к 30-м годам ХХ столетия. Одними из первых, исследовавшими в общей форме задачи линейного программирования, были: Джон фон Нейман, знаменитый математик и физик, доказавший основную теорему о матричных играх и изучивший экономическую модель, носящую его имя; советский академик, лауреат Нобелевской премии (1975 г.) Л. В. Канторович, сформулировавший ряд задач линейного программирования и предложивший (1939 г.) метод их решения (метод разрешающих множителей), незначительно отличающийся от симплекс-метода.

В 1931 г. венгерский математик Б. Эгервари рассмотрел математическую постановку и решил задачу линейного программирования, имеющую название «проблема выбора», метод решения получил название «венгерского метода».

Л. В. Канторовичем совместно с М. К. Гавуриным в 1949 г разработан метод потенциалов, который применяется при решении транспортных задач. В последующих работах Л. В. Канторовича, В. С. Немчинова, В. В. Новожилова, А. Л. Лурье, А. Брудно, А. Г. Аганбегяна, Д. Б. Юдина, Е. Г. Гольштейна и других математиков и экономистов получили дальнейшее развитие как математическая теория линейного и нелинейного программирования, так и приложение её методов к исследованию различных экономических проблем. Методам линейного программирования посвящено много работ зарубежных ученых. В 1941 г. Ф. Л. Хитчкок поставил транспортную задачу. Основной метод решения задач линейного программирования — симплекс-метод — был опубликован в 1949 г Дж. Данцигом. Дальнейшее развитие методы линейного и нелинейного программирования получили в работах Г. Куна (англ.), А. Таккера (англ.), Гасса (Gass S. I.), Чарнеса (Charnes A.), Била (Beale E. M.) и др.

Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция, либо ограничения, либо то и другое нелинейны. В 1951 г была опубликована работа Куна и Таккера, в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области.

Начиная с 1955 г опубликовано много работ, посвященных квадратическому программированию (работы Била, Э. Баранкина (Barankin E.) и Дорфмана (Dorfman R.), Франка (Frank M.) и Вольфа (Wolfe P.), Г. Марковица и др.). В работах Денниса (Dennis J. B.), Розена (Rosen J. B.) и Зонтендейка (Zontendijk G.) разработаны градиентные методы решения задач нелинейного программирования.

В настоящее время для эффективного применения методов математического программирования и решения задач на компьютерах разработаны алгебраические языки моделирования, представителями которыми являются AMPL и LINGO.

Править] Литература

Абакаров А.Ш., Сушков Ю.А. Статистическое исследование одного алгоритма глобальной оптимизации. — Труды ФОРА, 2004.
Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. пец. вузов. — М.: Высшая школа, 1986.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
Жиглявский А.А., Жилинкас А.Г. Методы поиска глобального экстремума. — М.: Наука, Физматлит, 1991.
Карманов В.Г. Математическое программирование = Математическое программирование. — Изд-во физ.-мат. литературы, 2004.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
Плотников А.Д. Математическое программирование = экспресс-курс. — 2006. — С. 171. — ISBN 985-475-186-4
Растригин Л.А. Статистические методы поиска. — М.: 1968.
Хемди А. Таха Введение в исследование операций = Operations Research: An Introduction. — 8 изд.. — М.: «Вильямс», 2007. — С. 912. — ISBN 0-13-032374-8

[скрыть] п·о·р Методы оптимизации
Одномерные	Метод золотого сечения • Деление пополам • Дихотомия • Метод парабол • Перебор по сетке • Метод Фибоначчи • Троичный поиск
Прямые методы	Метод Гаусса • Метод Нелдера — Мида • Метод сопряжённых направлений • Метод Хука — Дживса • Метод конфигураций • Метод Розенброка
Первого порядка	Градиентный спуск • Покоординатный спуск • Метод сопряжённых градиентов • Квазиньютоновские методы
Второго порядка	Метод Ньютона • Метод Ньютона — Рафсона
Стохастические	Метод Монте-Карло • Имитация отжига • Эволюционные алгоритмы • Генетические алгоритмы • Дифференциальная эволюция • Муравьиный алгоритм • Метод роя частиц
Методы линейного программирования	Симплекс-метод • Метод эллипсоидов • Метод потенциалов

Методы оптимизации (базовый курс)

Глава 1. Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве

1.1. Область допустимых значений вектора управляемых параметров Х

Тест: Область допустимых значений. Тест 1

Тест: Область допустимых значений. Тест 2

Тест: Область допустимых значений. Тест 3

Тест: Область допустимых значений. Тест 4

1.2. Выпуклое множество допустимых значений вектора варьируемых параметров

1.3. Постановка детерминированной задачи оптимизации

1.4. Классификация критериев оптимальности

1.5. Свойства выпуклых критериев оптимальности

1.6. Классификация детерминированных задач оптимизации.

Глава 2. Условия существования минимума в детериминированных задачах оптимизации

2.1. Одномерная задача оптимизации

2.2. Многомерная задача безусловной оптимизации

2.3. Задача выпуклого программирования

2.4. Задача нелинейного программирования с ограничениями типа равенств

2.5. Теорема Куна-Таккера для задачи нелинейного программирования с ограничениями типа неравенств

2.6. Теорема Куна-Таккера для общей задачи нелинейного программирования

2.7. Аналитическое решение многомерных задач нелинейного программирования

Тест: Аналитическое решение задачи НП. Тест 1

Тест: Аналитическое решение задачи НП. Тест 2

Глава 3. Классификация поисковых методов оптимизации и методология их сравнения

3.1. Классификация методов решения детерминированных задач оптимизации

Тест: Итерационная формула метода решения детерминированной задачи НП. Тест 1

Тест: Итерационная формула метода решения детерминированной задачи НП. Тест 2

3.2. Наилучшие алгоритмы оптимизации

3.3. Экспериментальное тестирование алгоритмов оптимизации

3.4. Классы тестовых функций

Тест: Генерация тестовых функций. Тест 1

Тест: Генерация тестовых функций. Тест 2

Глава 4. Методы поиска минимума одномерных унимодальных функций

4.1. Алгоритм равномерного поиска

4.2. Алгоритм деления пополам

4.3. Алгоритм Фибоначчи

Тест: Алгоритм Фибоначчи. Тест 1

4.4. Алгоритм золотого сечения

4.5. Сравнение эффективности алгоритмов одномерной условной оптимизации

4.6. Метод квадратичной аппроксимации

4.7. Метод Паулла

4.8. Методы на основе поиска стационарной точки критерия оптимальности

4.9. Повышение эффективности поиска на основе дополнительной информации о свойствах критерия оптимальности

Глава 5. Методы поиска глобального минимума одномерных многоэкстремальных функций

5.1. Метод перебора. Одномерный метод Монте-Карло

5.2. Метод выделения интервалов унимодальности

5.3. Метод аппроксимирующих моделей

Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы

6.1. Метод Гаусса-Зейделя

Тест: Метод Гаусса-Зейделя. Тест 1

6.2. Метод Хука-Дживса

6.3. Метод Розенброка

6.4. Метод сопряженных направлений

6.5. Симплекс-метод

6.6. Метод деформируемого многогранника (Нелдера-Мида)

Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков

7.1. Метод наискорейшего спуска. Метод дробления шага

Тест: Градиентный метод с дроблением шага. Тест 1

7.2. Метод оптимизации Ньютона

Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска

8.1. Метод с возвратом при неудачном шаге. Метод наилучшей пробы

8.2. Метод комплексов

8.3. Метод повторяющегося случайного поиска

8.4. Метод случайного поиска с постоянным радиусом поиска и случайными направлениями

Глава 9. Многомерная локальная условная оптимизация

9.1. Методы последовательной безусловной оптимизации

9.2. Метод скользящего допуска

9.3. Модифицированный метод комплексов

9.4. Метод линейной аппроксимации

9.5. Метод проекции градиента

Тест: Проектирование точки на множество. Тест 1

Тест: Проектирование точки на множество. Тест 2

Тест: Проектирование точки на множество. Тест 3

Глава 10. Многомерная глобальная условная оптимизация

10.1. Метод сведения к совокупности вложенных задач глобальной одномерной минимизации

10.2. Метод сведения к задаче одномерной глобальной оптимизации с помощью развертки Пеано

10.3. Метод Монте-Карло

Глава 11. Задачи многокритериальной оптимизации и методы их решения

11.1. Постановка задачи многокритериальной оптимизацию. Множество Парето

Тест: Множество Парето. Тест 1

11.2. Метод весовых множителей решения задачи многокритериальной оптимизации

11.3. Метод эпсилон-ограничений решения задачи многокритериальной оптимизации

11.4. Метод справедливого компромисса для решения задач многокритериальной оптимизации

11.5. Метод приближения к идеальному решению для решения задач многокритериальной оптимизации

11.6. Метод последовательных уступок для решения задач многокритериальной оптимизации

Глава 12. Задачи оптимального управления и методы их приближенного решения

12.1. Постановка задачи оптимального управления

Тест: Постановка задачи оптимального управления. Тест 1

12.2. Принцип максимума Л. С. Понтрягина

12.3. Метод решения задачи оптимального управления, использующий П-систему

12.4. Решение задачи оптимального управления методом вариаций в фазовом пространстве

12.5. Решение задачи оптимального управления методом вариаций в пространстве управлений

12.6. Метод динамического программирования Беллмана

12.7. Решение задачи оптимального управления методом динамического программирования Беллмана

Тест: Решение задачи оптимального управления методом динамического программирования Беллмана. Тест 1

12.8. Решение задачи оптимального управления методом сведения к задаче нелинейного программирования

Тест: Решение задачи оптимального управления путем сведения к задаче нелинейного программирования. Тест 1

МЕТОДИКА И МОДЕЛИ ОПТИМИЗАЦИИ ВХОДНЫХ ПАРАМЕТРОВ ТЕХНОЛОГИЧЕСКОЙ ЦЕПИ ХЛЕБОПРОДУКТОВОГО ОБЪЕДИНЕНИЯ

Лойко В.И. – д.т.н., профессор

Кубанский государственный аграрный университет

Першакова Т.В. – к. т. н., доцент

Ищенко О.В. – старший преподаватель

Краснодарский кооперативный институт (филиал БУПК)

В статье предлагается методика и модели оптимизации входных параметров технологической цепи хлебопродуктового объединения потребительской кооперации.

Рассмотрим наиболее типичные вертикально интегрированные структуры хлебопродуктовых объединений потребительской кооперации (рис. 1, 5 в [1]).

Годовой объем необходимого сырья для переработки, а значит и годовой объем финансовых средств для закупки может быть рассчитан, исходя из годового спроса на хлебопекарную продукцию сегмента рынка потребительской кооперации. Если сразу закупить (или произвести) годовой объем исходного продукта переработки (в [1] для структуры рис. 5 это зерно, а для структуры рис. 1 – мука), то за год будет реализован всего один цикл. В этом случае сразу возникает почти неразрешимая проблема (как финансовая, так и складская) хранения такого большого объема запасов. Если же производить закупки мелкими партиями (большое число циклов в году), проблемой станут резко увеличившиеся затраты, связанные с частыми заказами (документация, транспортировка, погрузочно-разгрузочные работы и т.п.).

Таким образом, возникает задача оптимизации числа циклов m и связанных с ним объемов финансового 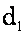и материального 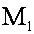потоков.

Как указывалось в [1], число циклов может быть определено по количеству поставок исходного для производства сырья в течение года. Для закупки и организации поставки необходимо возникновение исходного финансового потока 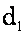, компенсирующего произведенные начальные издержки и, таким образом, запускающего производственный цикл вертикально интегрированной системы.

Для бесперебойного функционирования технологической цепи необходимо, чтобы на входе каждого ее звена в любой производственный момент времени находилось достаточное количество исходного для переработки сырья или, другими словами, запасов. Поскольку производственные запасы в течение технологического процесса расходуются, то их необходимо возобновлять. С этой целью вновь создается финансовый поток 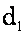, инициирующий возобновление уменьшившихся до минимального уровня производственных запасов, и так далее. Возникают типичные производственные циклы, причем их длительность и количество прямо связаны со скоростью расходования созданных в начале цикла запасов.

В связи с вышесказанным воспользуемся для определения числа циклов m и объемов исходных финансового 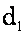и материального 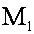потоков в вертикально интегрированной хлебопродуктовой производственной системе теорией управления запасами [3].

Необходимость запасов объясняется случайными процессами, протекающими в производственных системах. Нельзя быть уверенным в том, что продукты для переработки поступят на склад технологического звена именно в тот момент времени, когда они понадобятся. Если на некоторой стадии процесса производства потребуется какой-то вид сырья, а этого сырья не окажется в запасе, т. е. образовался дефицит, то процесс производства может задержаться или вообще остановиться.

Очевидно, что таких ситуаций необходимо по возможности избегать: на складах технологических звеньев (предприятий) хлебопродуктового объединения всегда должно быть нужное количество данного вида сырья. Однако если запасы увеличить, соответственно возрастет плата за их хранение. Управление запасами состоит в том, чтобы выбрать компромиссное или даже оптимальное решение при определенных условиях или ограничениях.

Независимо от того, какого рода систему управления запасами имеет производство, основные решения, которые может принять управляющий орган, состоят в следующем [3]:

- какое количество товара должно находиться в запасе;

- в какое время производить пополнение запаса.

Предметом исследования является связь между количеством Q запаса, имеющегося на складе производственного звена технологической цепи, и временем t, для которого рассматривается этот запас. Таким образом, мы исследуем функцию 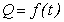, соответствующую величине запаса в момент времени t. Под Q будем понимать запасы только одного вида.

Дата добавления: 2016-01-04; просмотров: 24; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!